Tensors’rules if dimension > n x n

in linear algebra, is there many tensor (matrix dimension n x n x n) rules with exceptions in addition, substract, multiply, transpose that we don’t have in same operations with matrix less than dimension n x n?

In linear algebra, the rules for tensors (matrices with dimensions n x n x n) are essentially extensions of the rules that apply to matrices of smaller dimensions. However, there are some additional complexities and considerations that arise when dealing with tensors due to their higher-dimensional nature. Here are a few points to consider:

1. Tensor multiplication: While matrix multiplication is well-defined and straightforward for matrices of any size, tensor multiplication involves more complex operations such as tensor contraction (summing over specific indices) and outer product. These operations are not typically encountered when dealing with 3×3 matrices.
2. Transposition: Transposing a matrix involves flipping its rows and columns. For a 3×3 matrix, this is a relatively simple operation, but for higher-dimensional tensors, transposition can involve permuting more indices, leading to different effects on the tensor.
3. Addition and Subtraction: The addition and subtraction of tensors follow the same rules as matrices, i.e., element-wise addition/subtraction. However, for tensors of higher dimensions, the sizes must match along all axes for addition or subtraction to be valid.
4. Special Properties: Some properties that hold for matrices might not directly generalize to higher-dimensional tensors. For example, the determinant of a matrix is a scalar value, but for tensors, there are multiple notions of determinants depending on the type of tensor (e.g., for square matrices, it’s the standard determinant, but for higher-order tensors, it might involve more complex calculations).
5. Index Notation: Working with tensors often involves using index notation, which can be more intricate than the simple row-column notation used for matrices. This notation allows for concise representation and manipulation of tensors but may take some time to get used to.

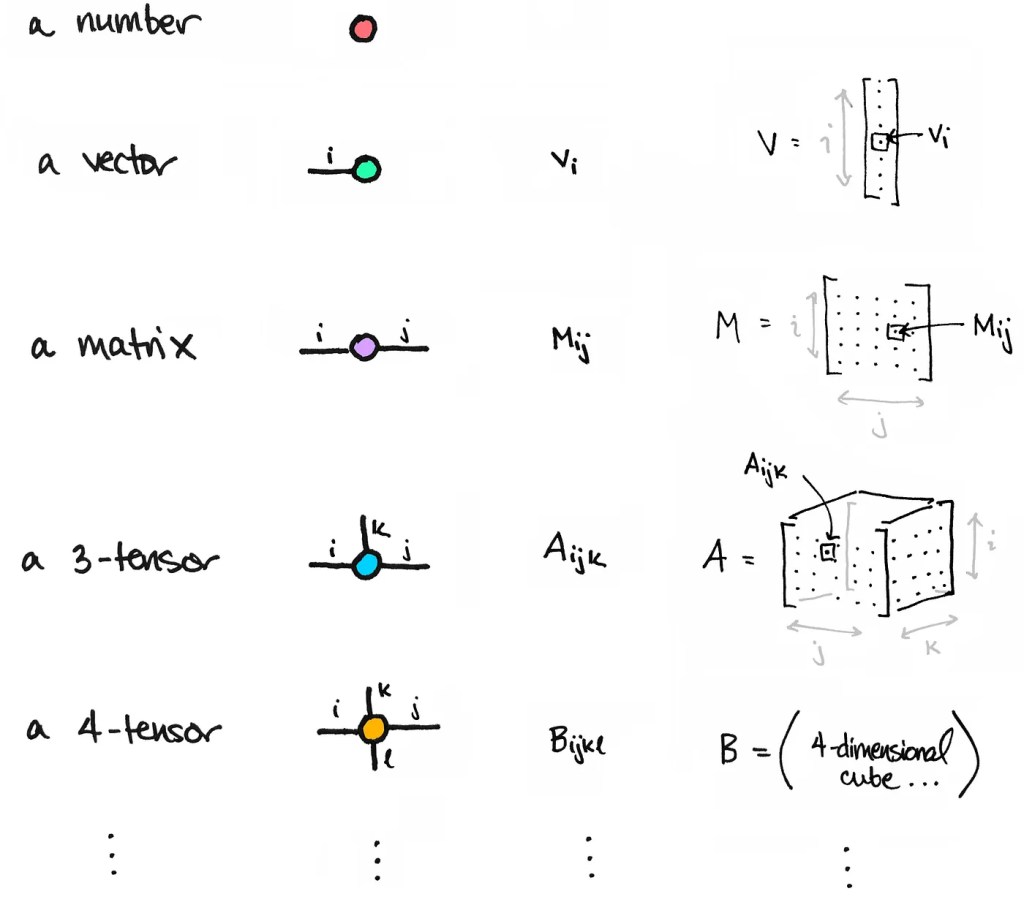
In summary, while the basic operations of addition, subtraction, multiplication, and transposition generalize from matrices to tensors, there are additional complexities and considerations that arise when dealing with tensors of higher dimensions. Understanding these nuances is important for working effectively with tensors in linear algebra.