Calculus: Notes de cours

• P: Preliminaires
• 1- Limites et continuités
• 2- Dérivées
• 3- Fonctions transcendantes
• 4- Applications sur la dérivée
• 5- Intégration
• 6- Techniques d’intégration
• 7- Applications sur l’intégration
• 8- Coniques, courbes paramétriques et polaires
• 9- Séquences, séries et séries de puissance
• 10- Vecteurs et coordonnées géométriques en 3D
• 11- Vecteurs
• 12- Dérivée partielle
• 13- Application sur la dérivée partielle
• 14- Intégration multiple
• 15- Champs de vecteurs
• 16- Calculs vectoriels
• 17- Exterior Calculus
• 18- Équations différentielles

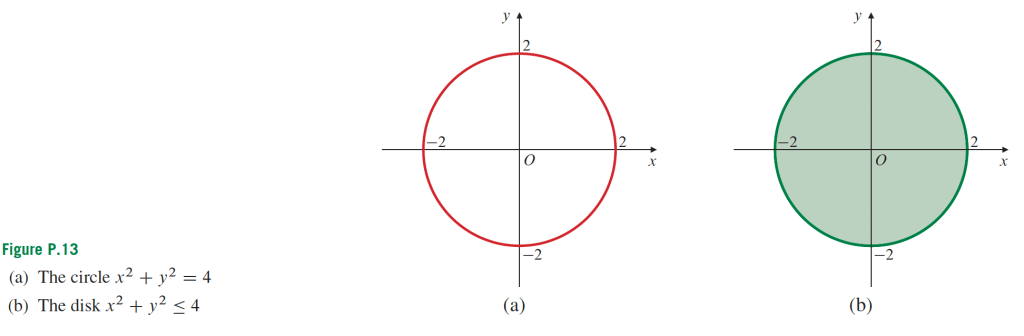
• La parabole possède un foyer, F.
• La parabole possède un sommet, S.
• La parabole possède une droite, appelée directrice.
• La droite perpendiculaire à la directrice de la parabole et qui passe par le foyer et le sommet est l’axe de symétrie.
• Le sommet S est équidistant au foyer F et à la directrice.

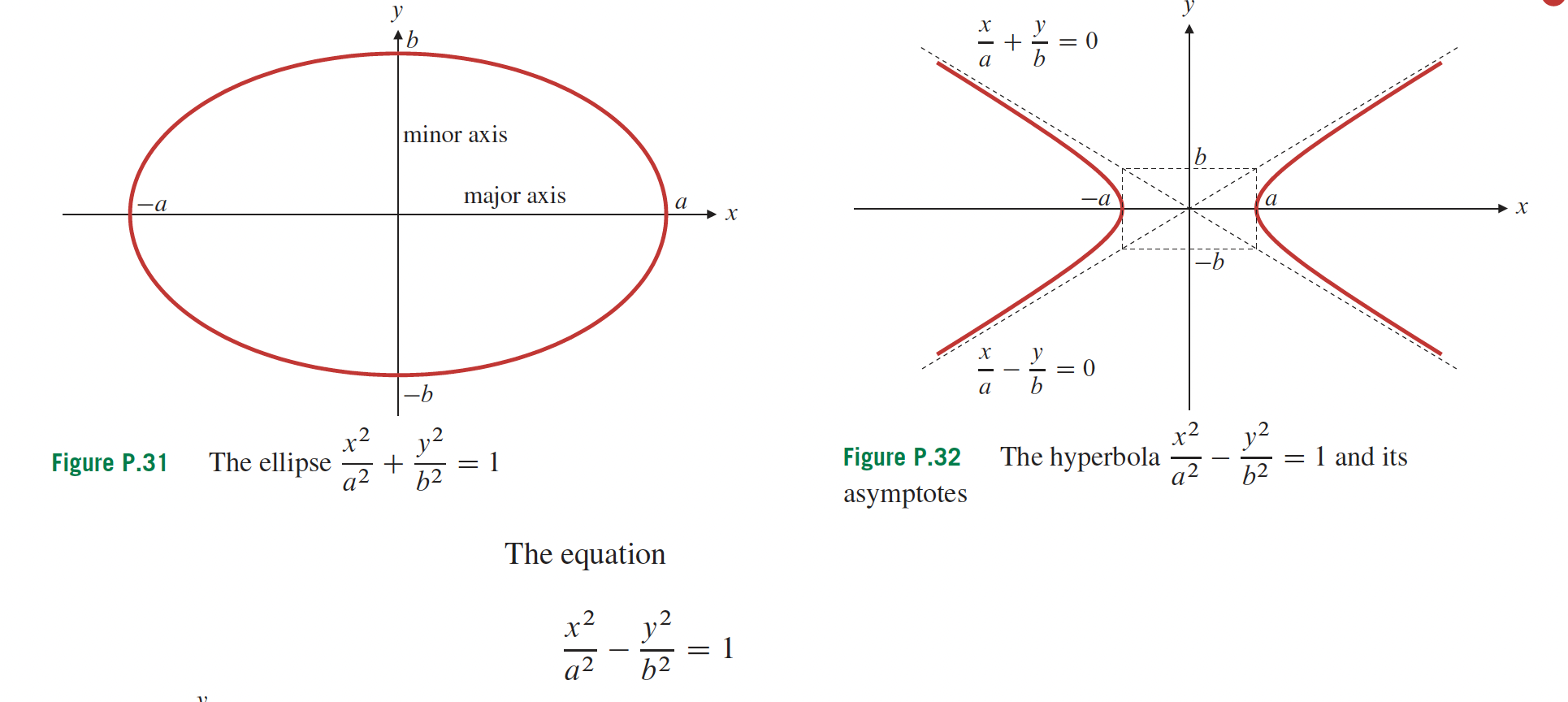
• L’hyperbole possède 2 sommets, S1 et S2..
• L’hyperbole possède 2 foyers, F1 et F2.
• L’hyperbole possède 2 asymptotes.
• La droite passant par les 2 foyers et les 2 sommets est l’axe transversal.
• La droite qui passe par le point d’intersection entre les asymptotes et qui est perpendiculaire à l’axe transversal est l’axe conjugué.
• On peut former un rectangle passant par les sommets de l’hyperbole et étant délimité par l’intersection avec les asymptotes.
• L’hyperbole peut être verticale ou horizontale.

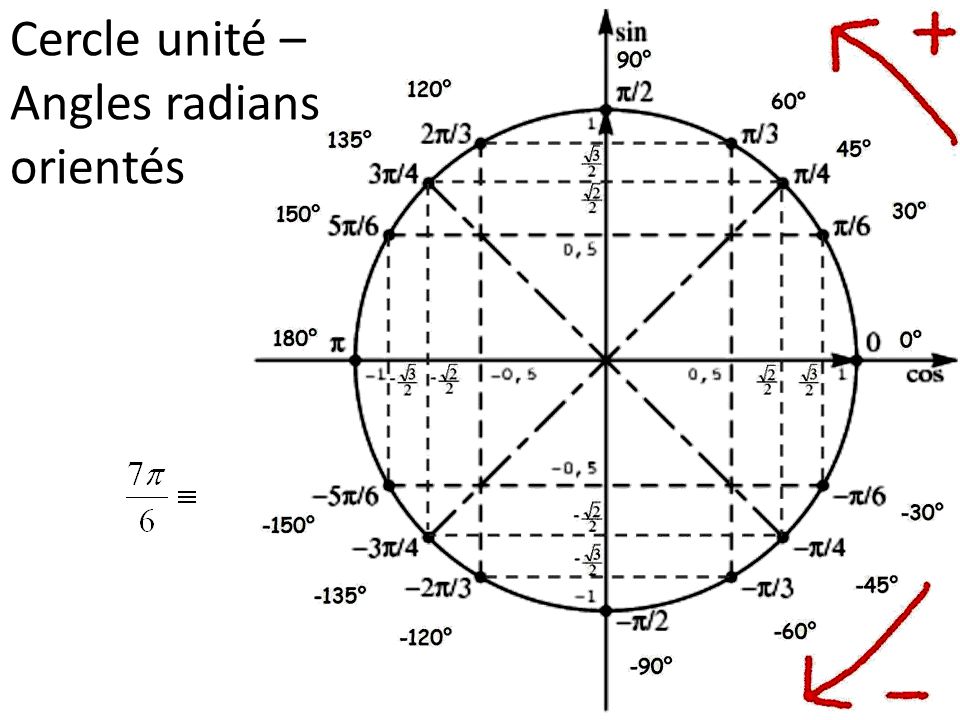
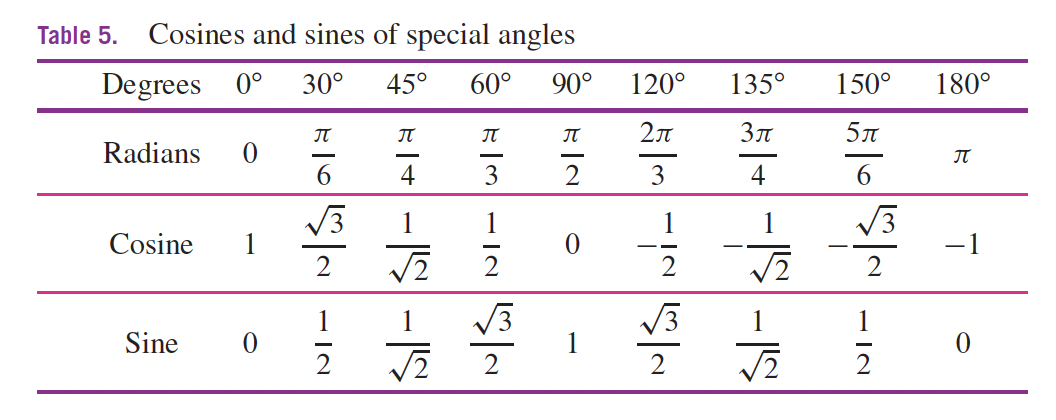
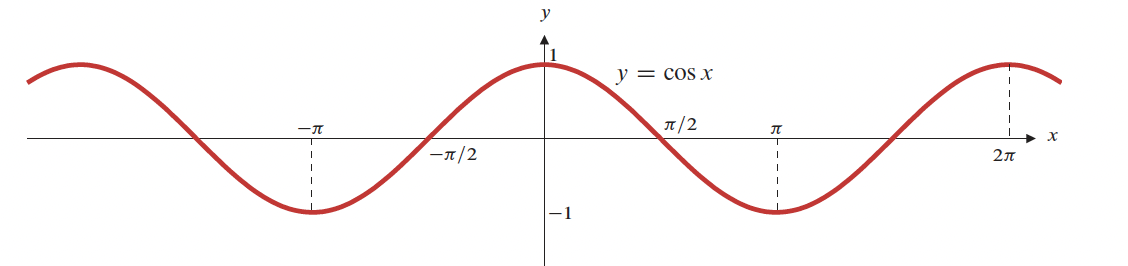
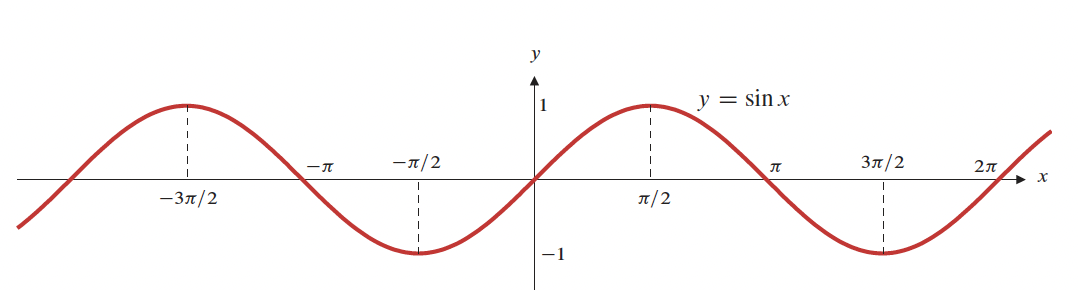
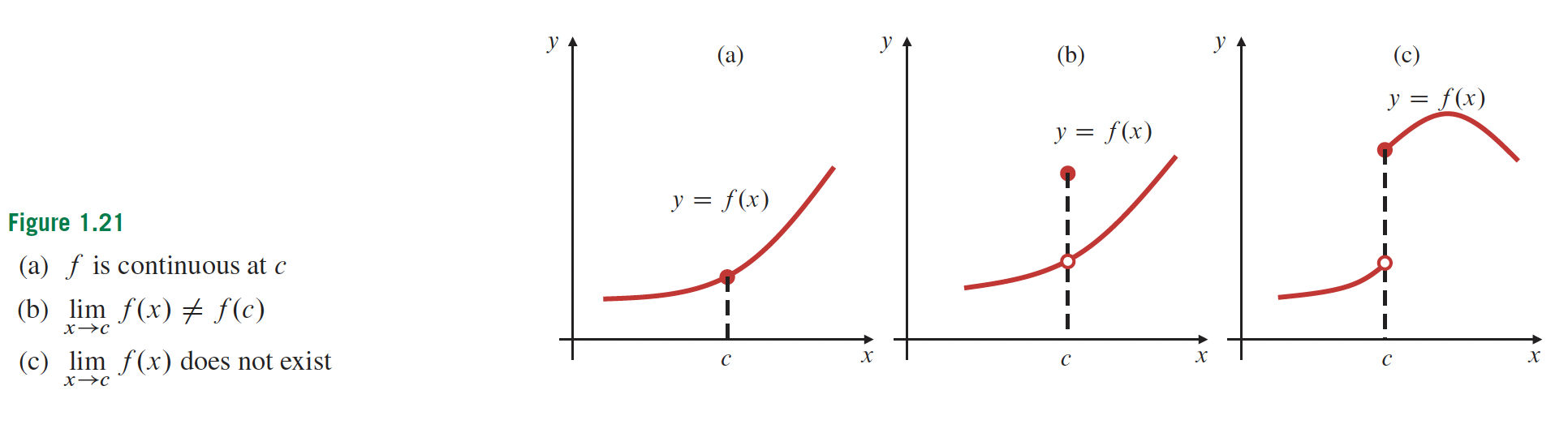
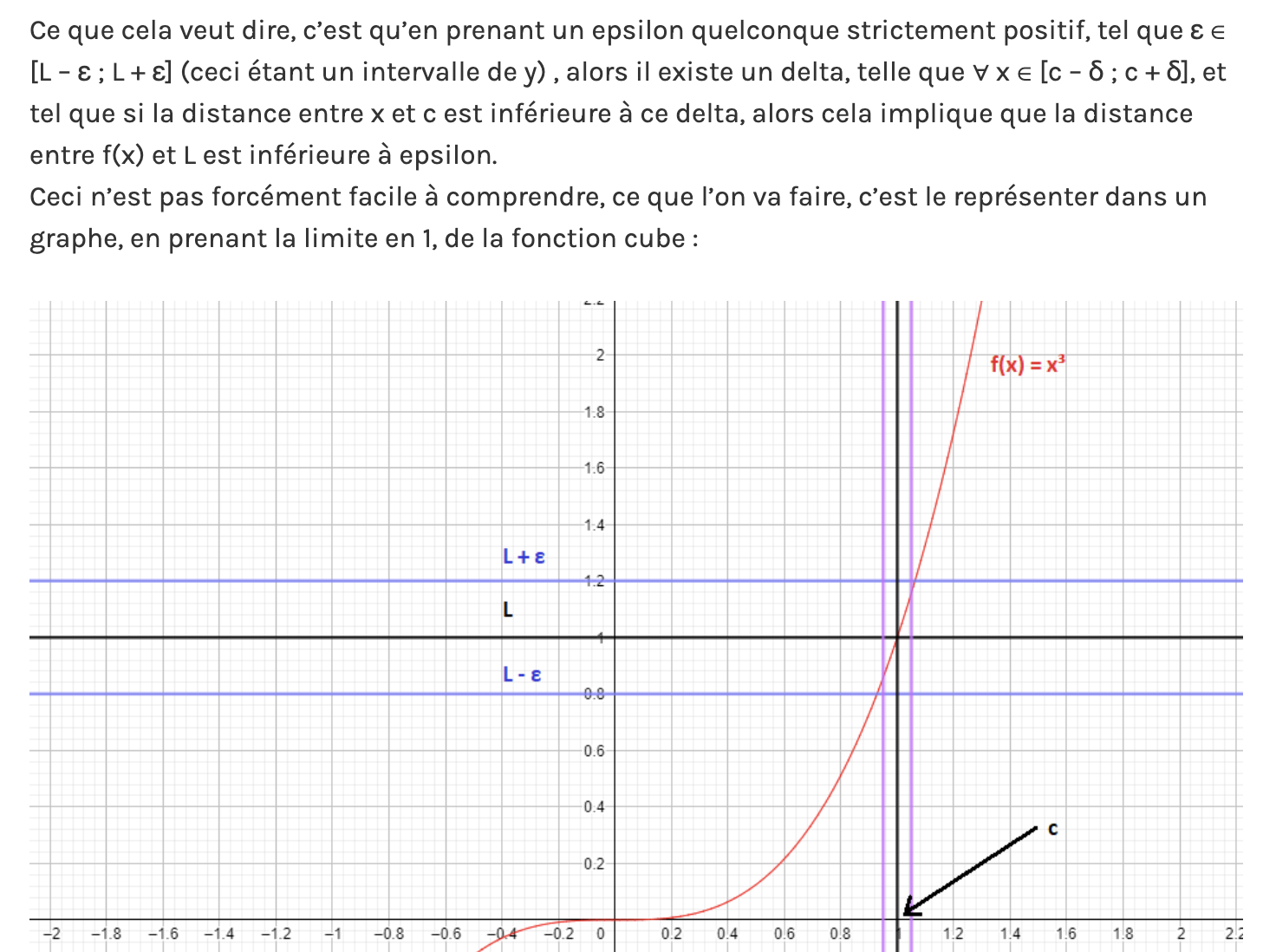
1- Limites et Continuités

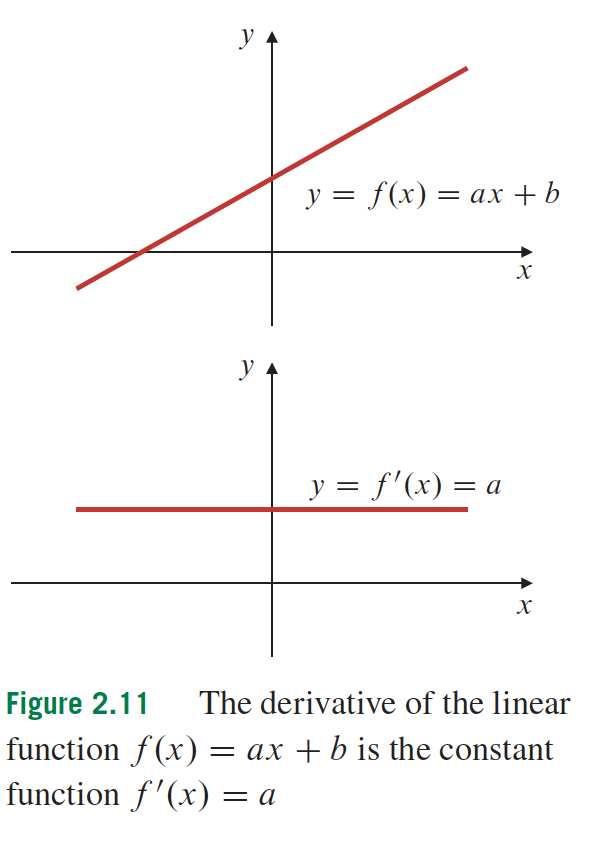
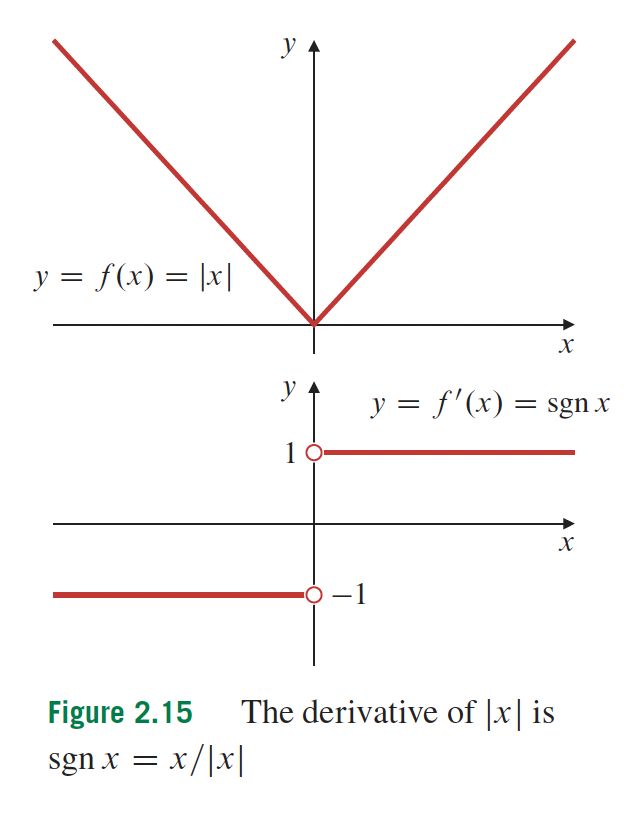
2- Différentiation

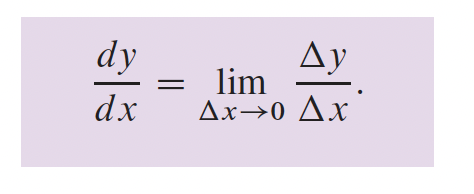
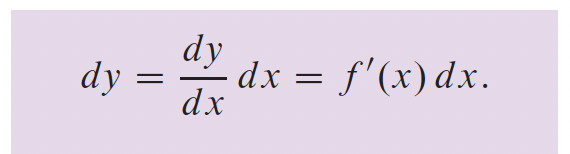
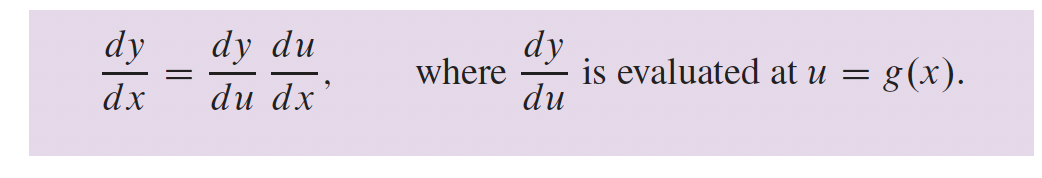
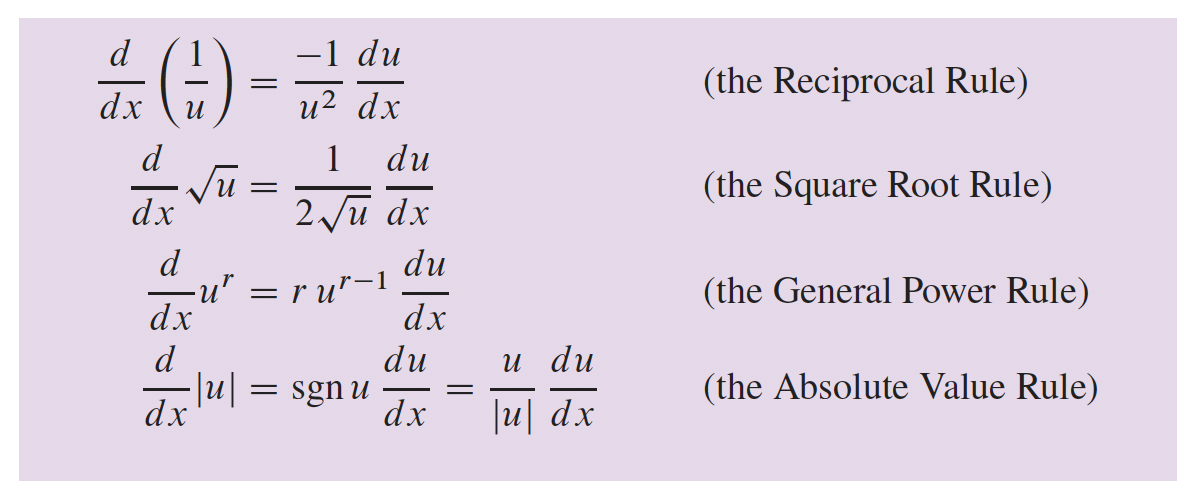
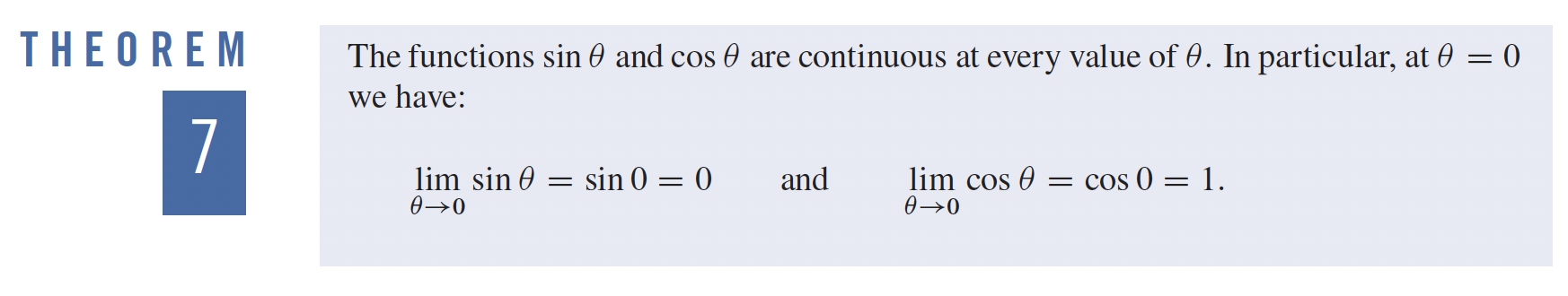
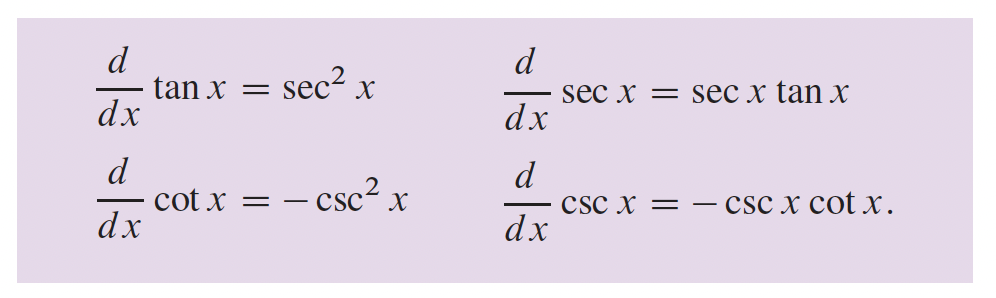
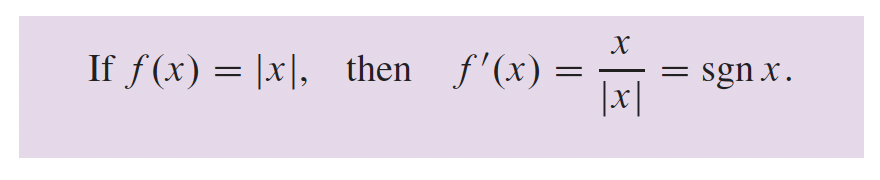
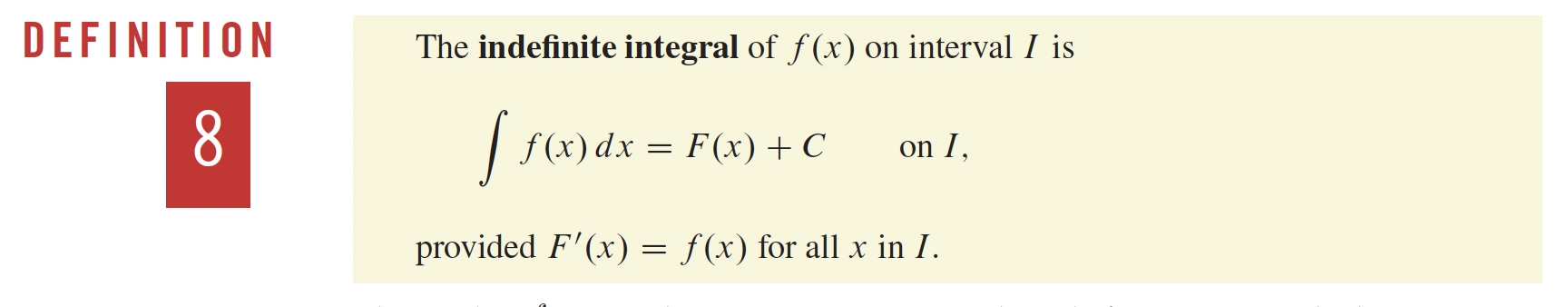
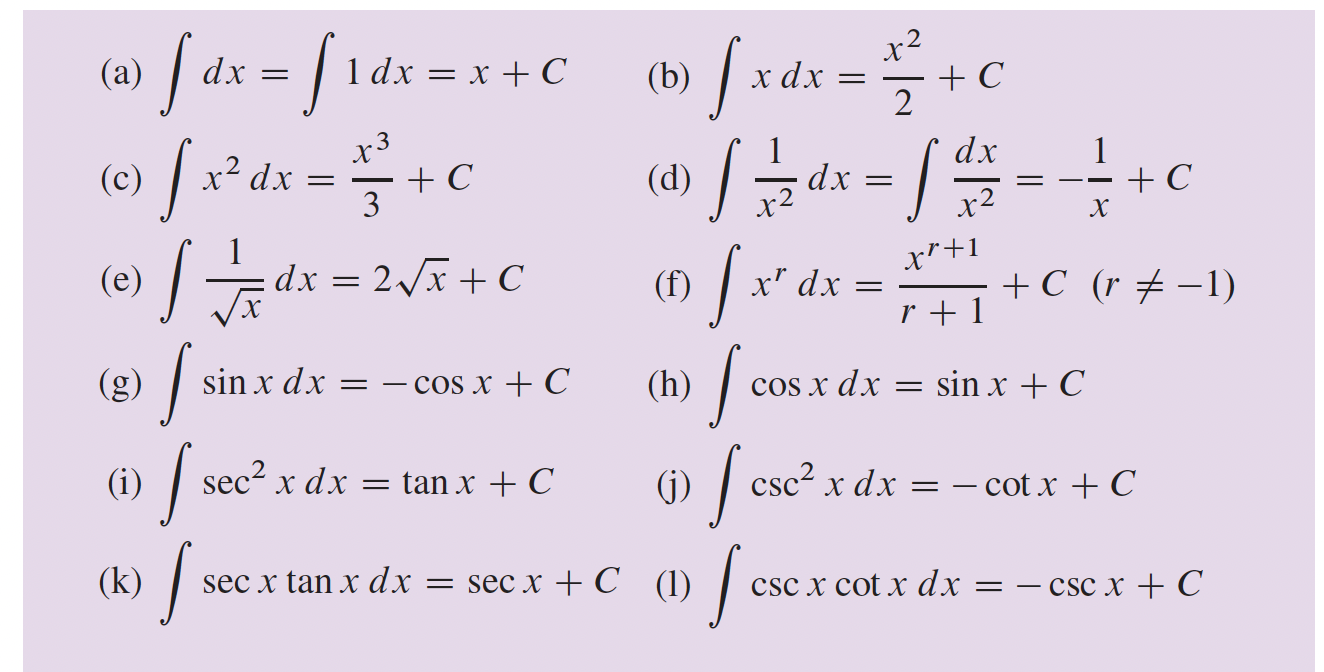
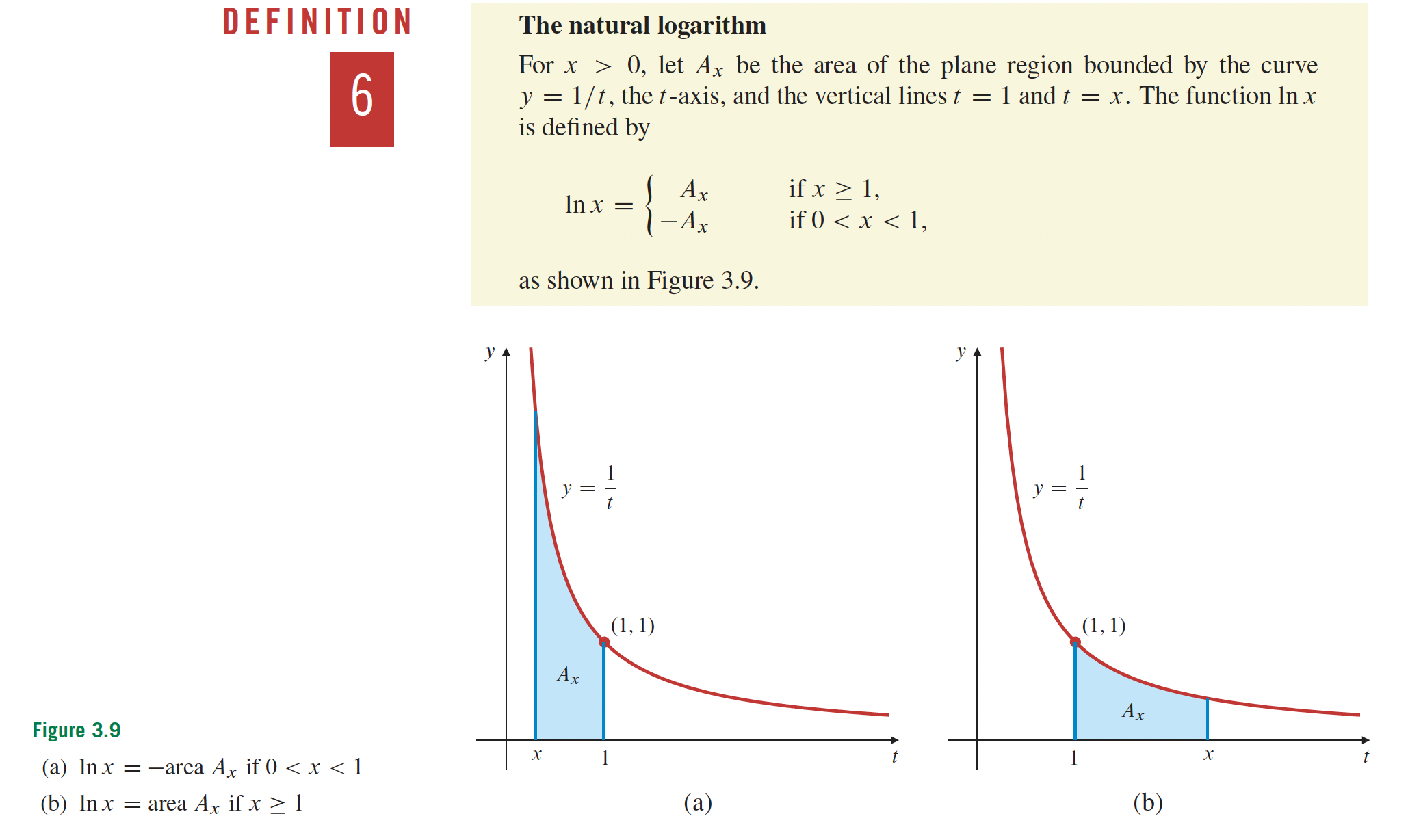
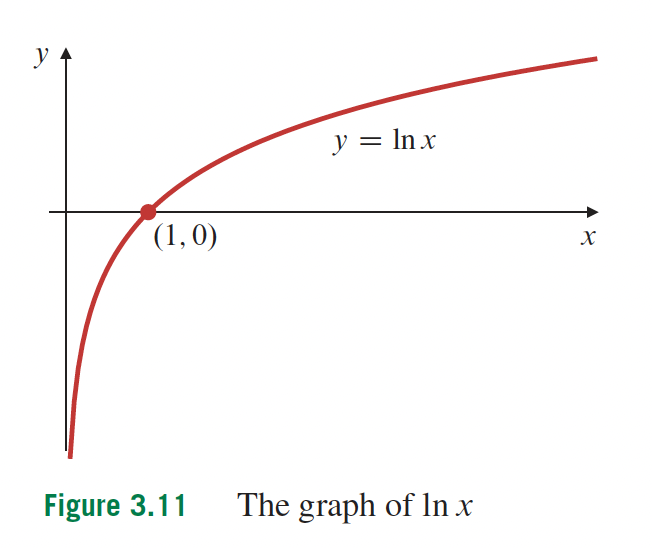
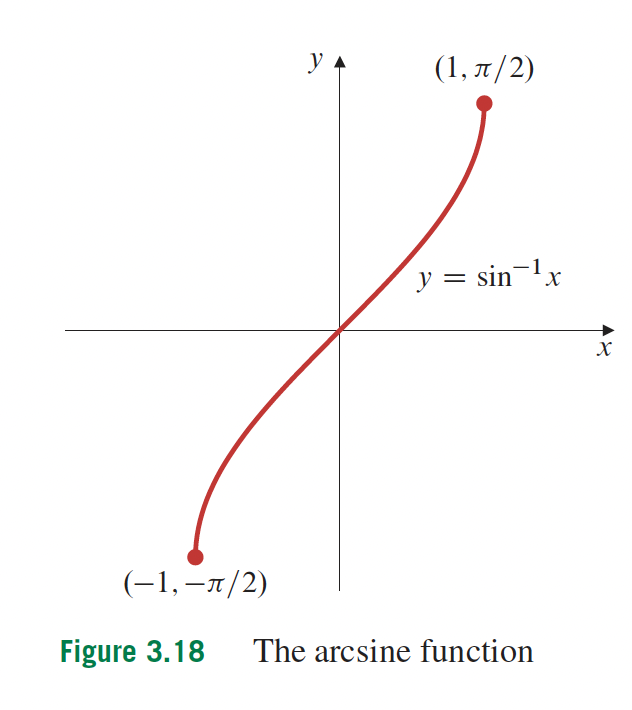
3- Fonctions transcendantes p.166

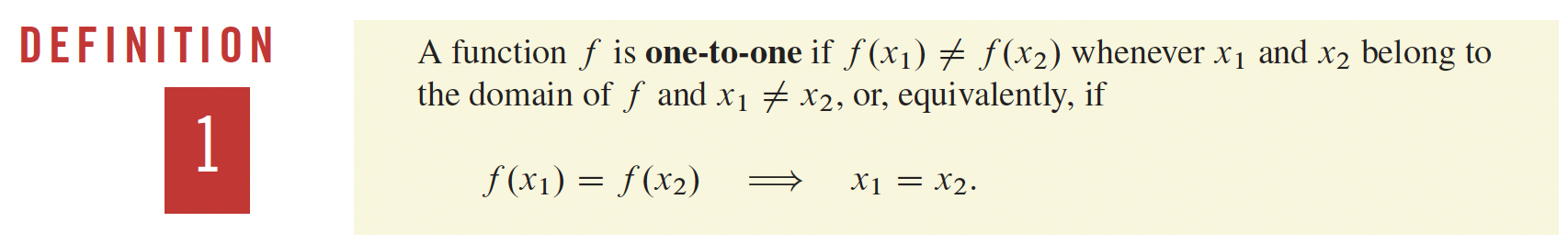
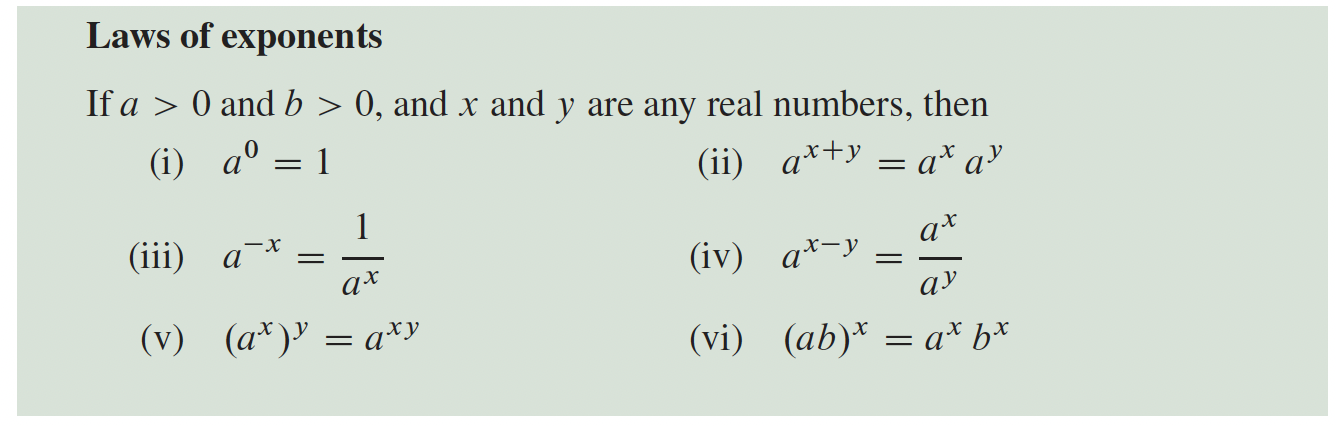
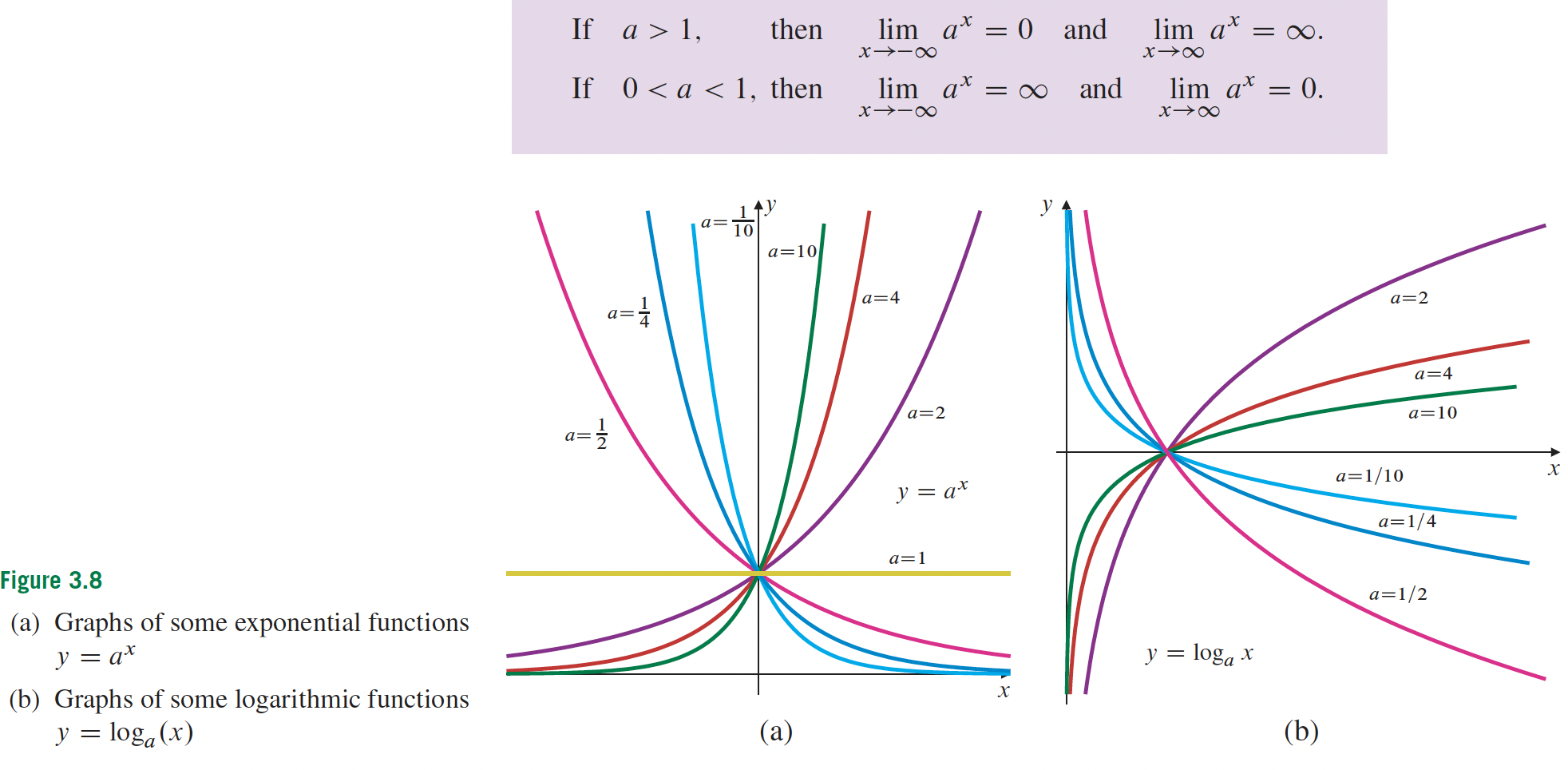
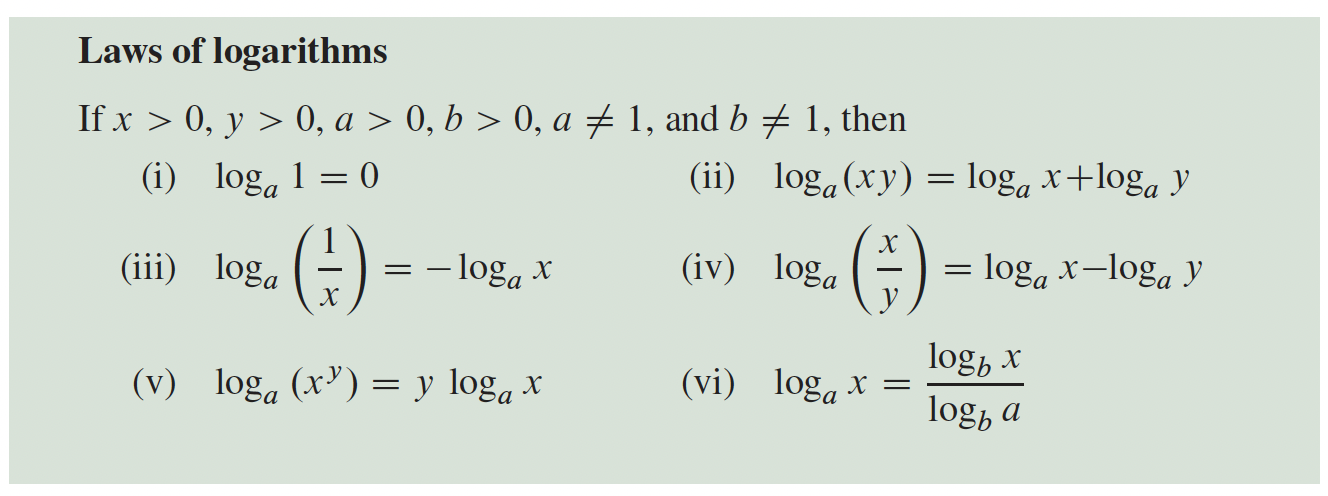
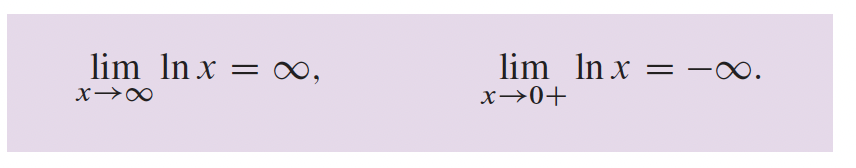
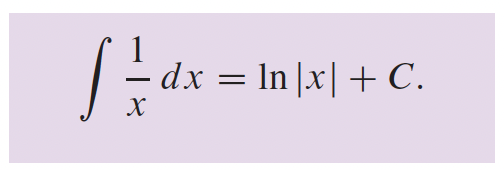
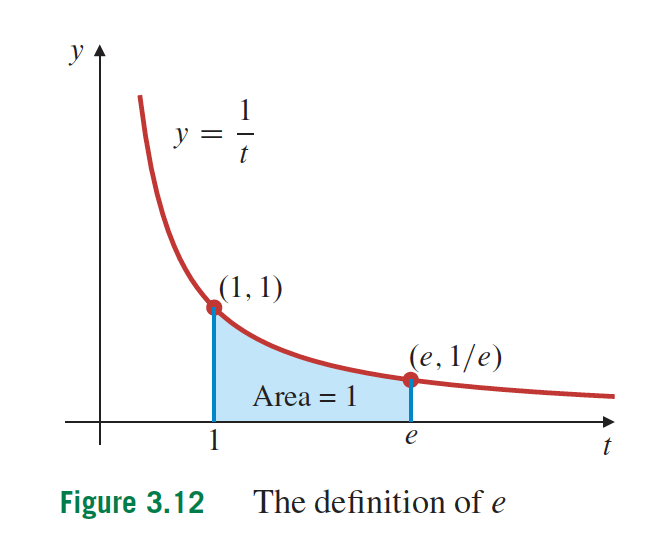
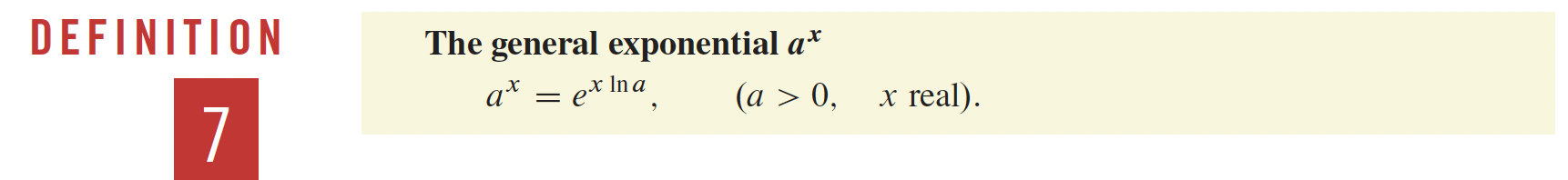
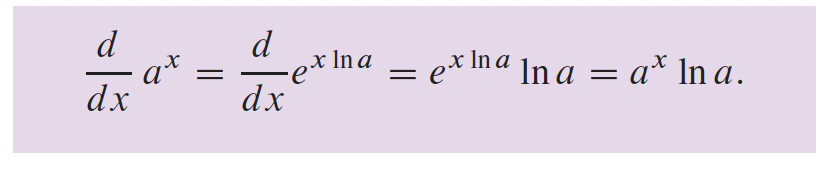
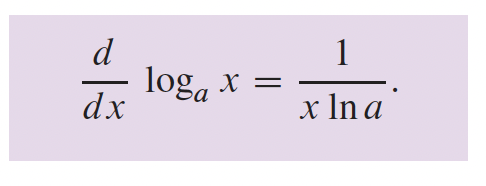
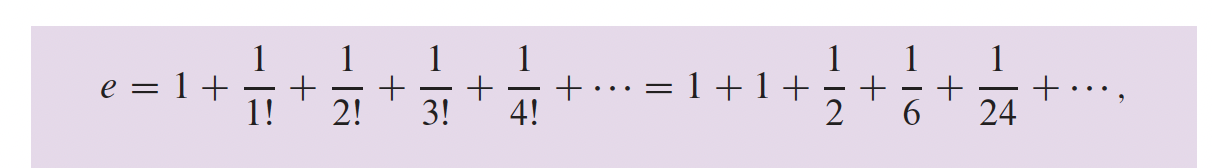
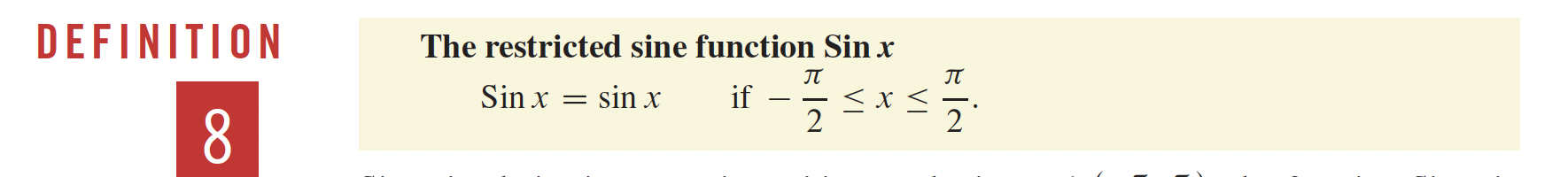
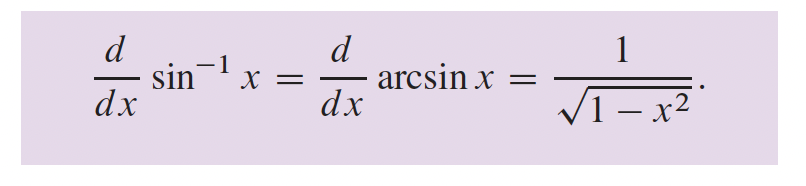
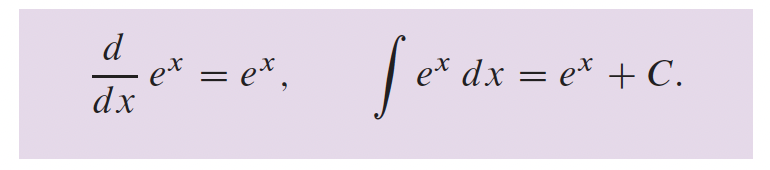
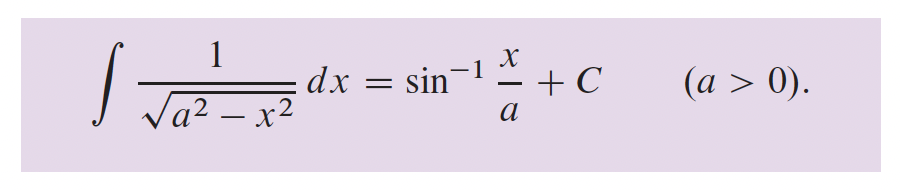
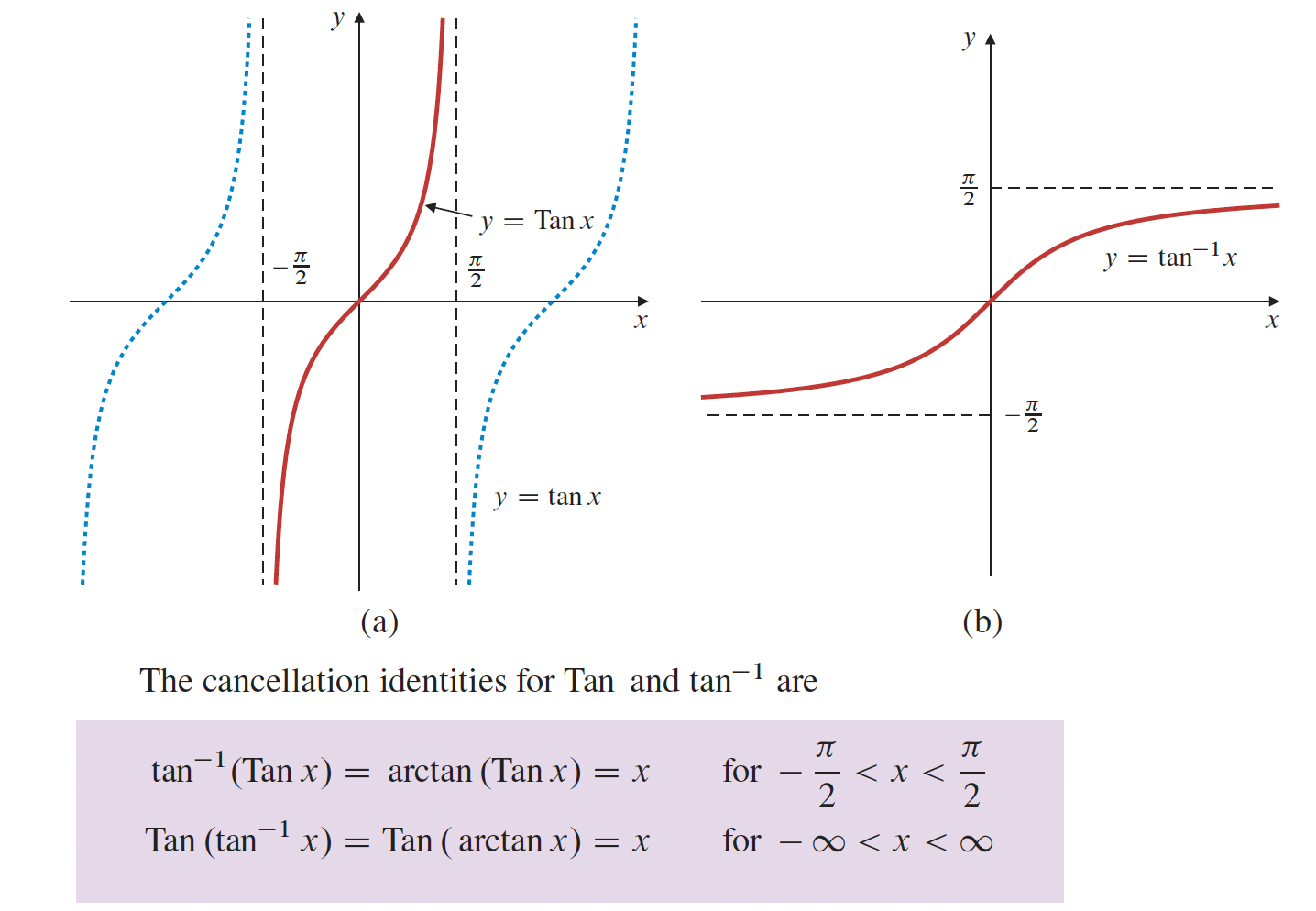
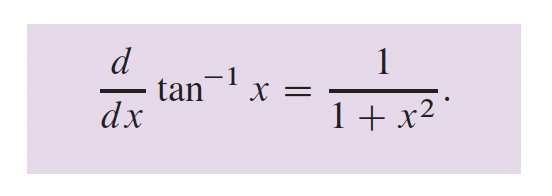
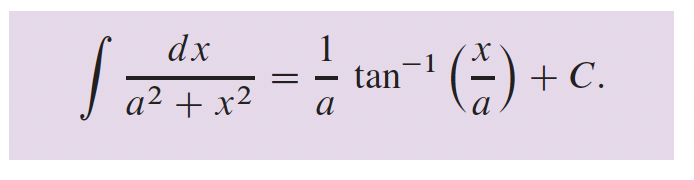
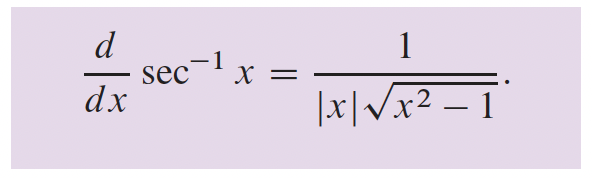
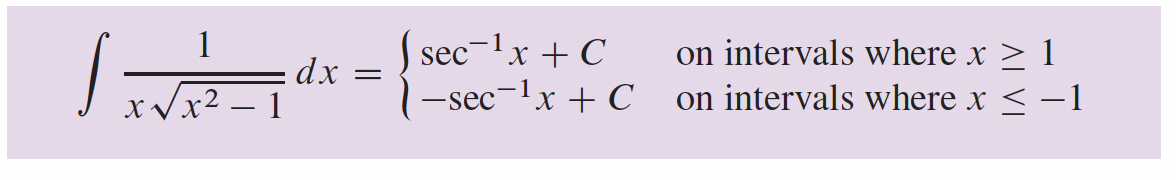
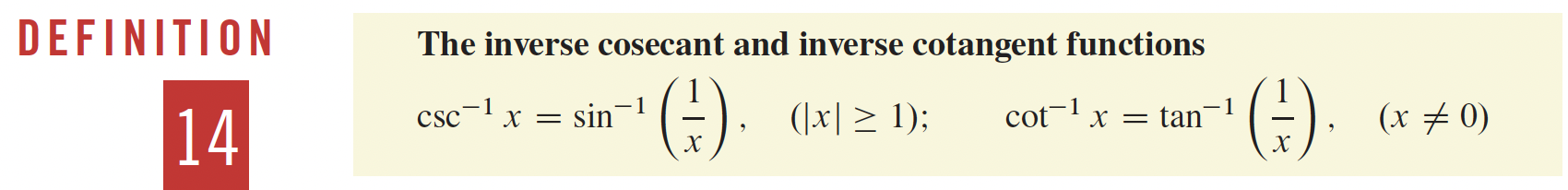
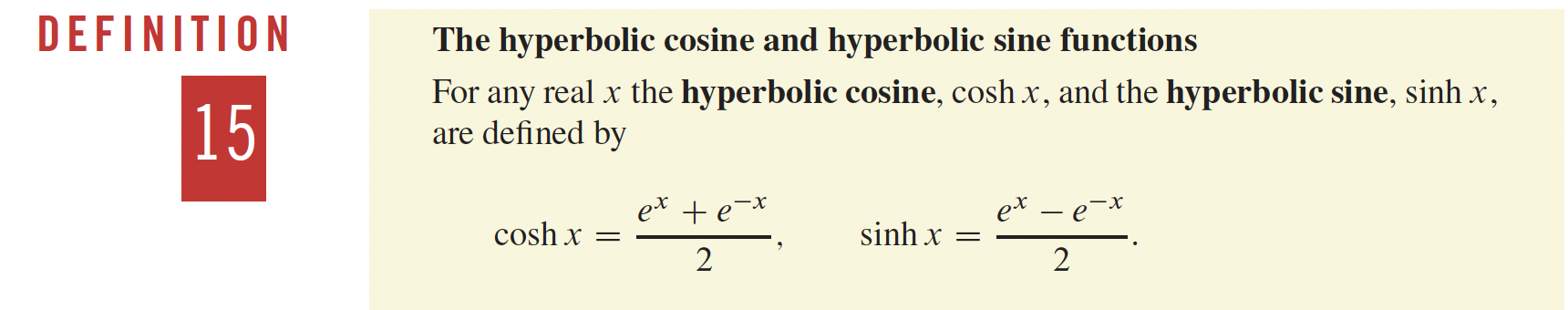
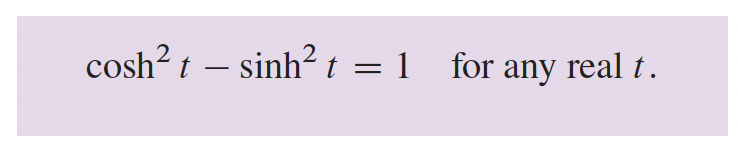
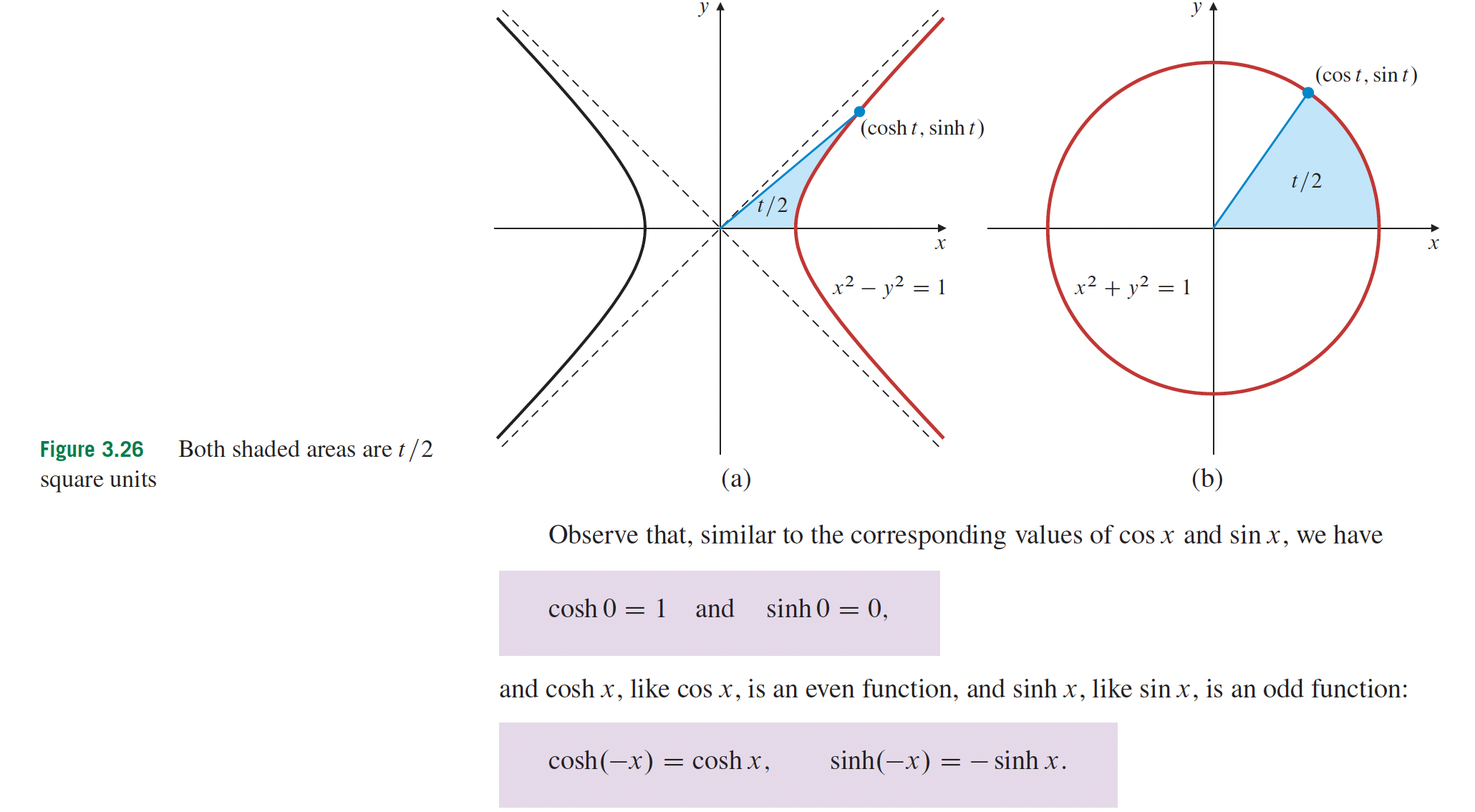
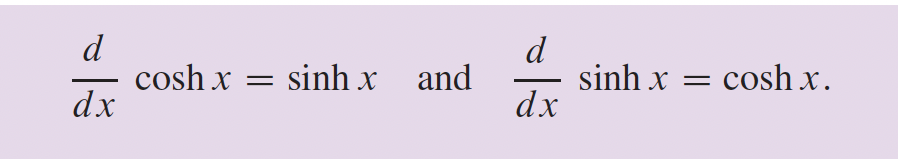
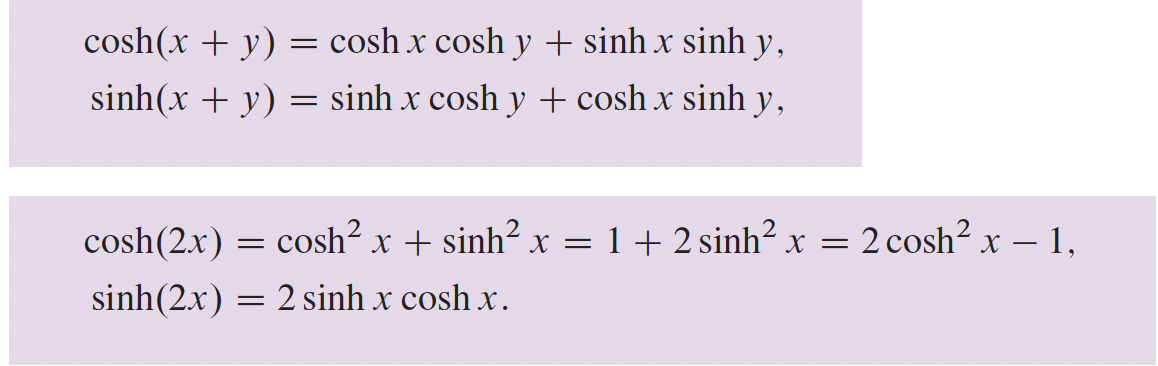
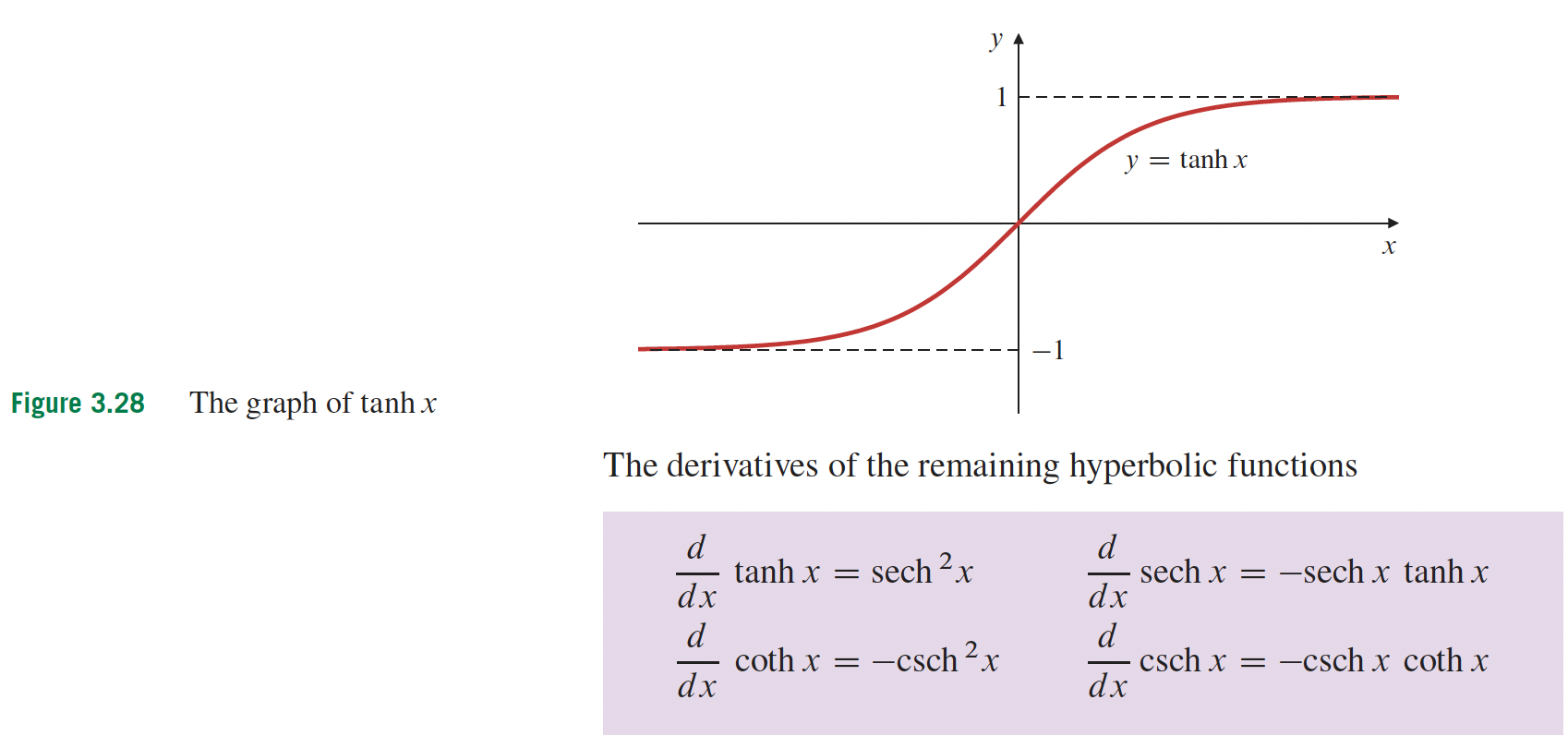
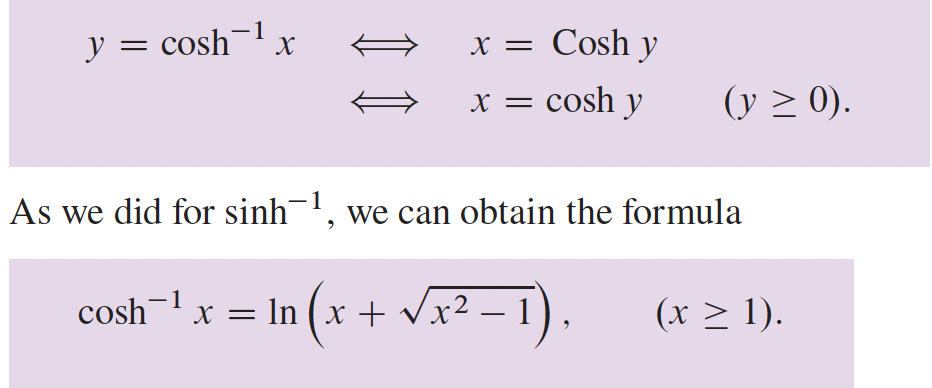
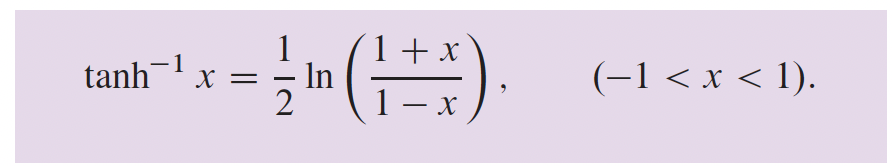
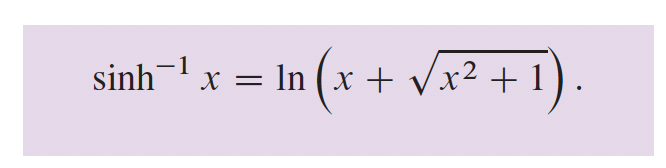
4- Applications sur les différentielles p.216

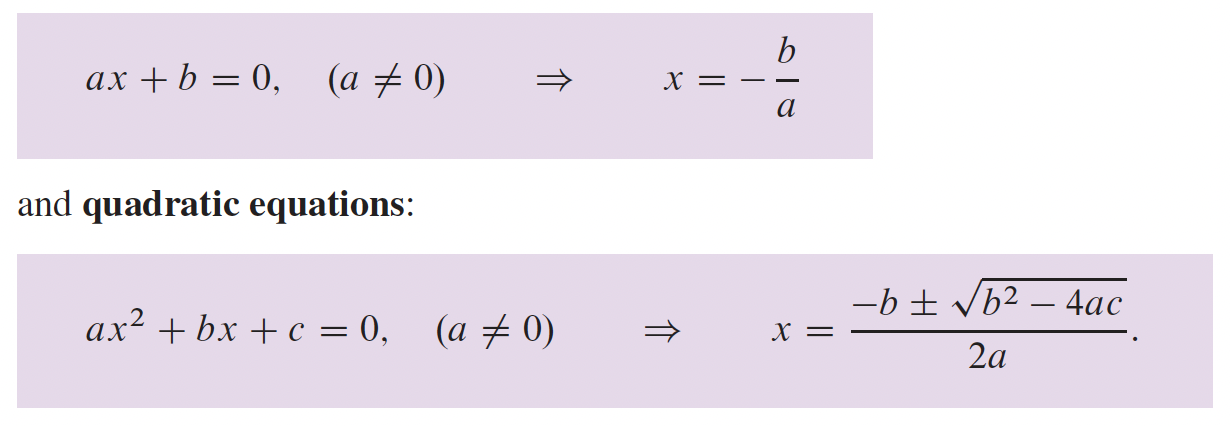
5- Intégration p. 291

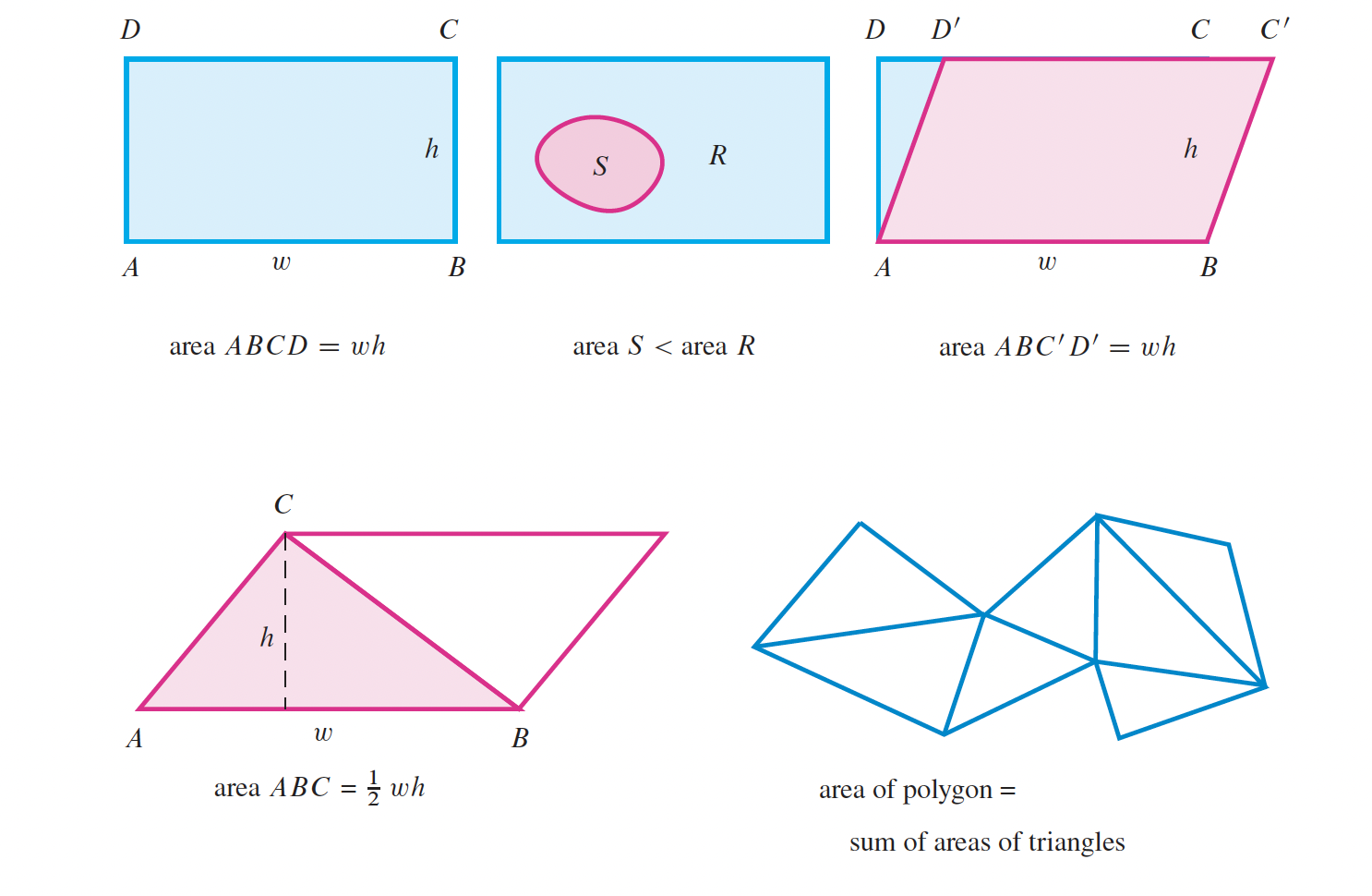
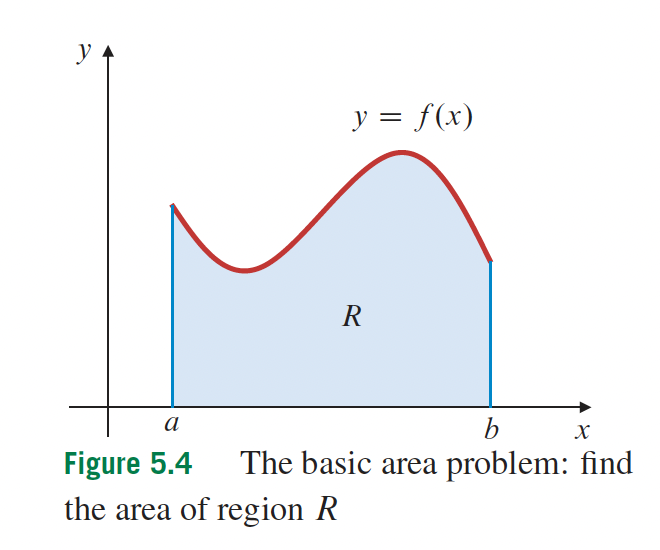
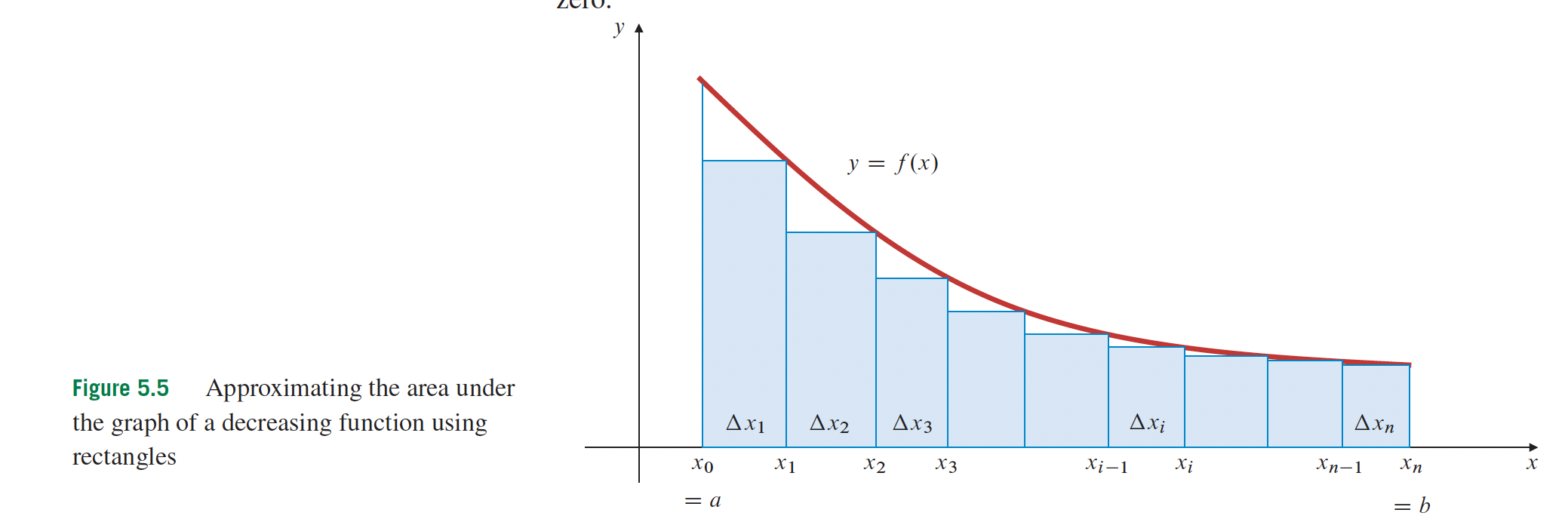
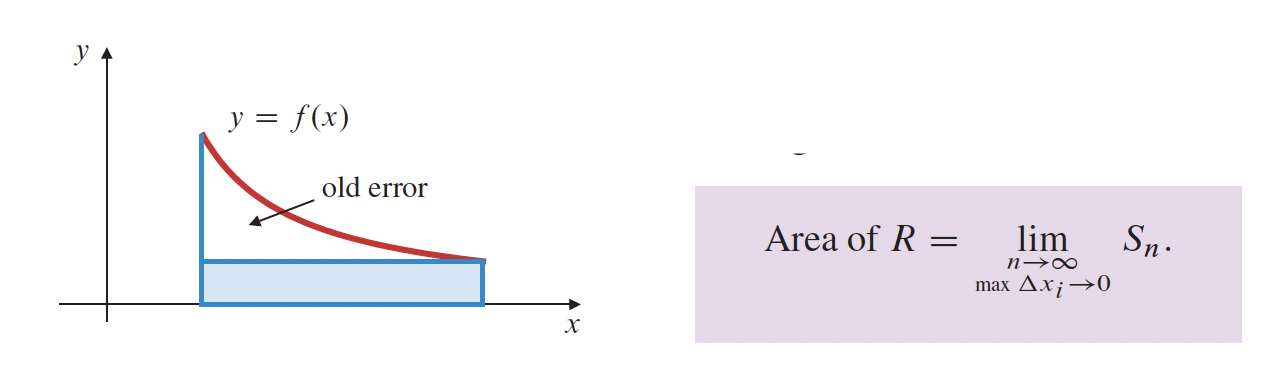
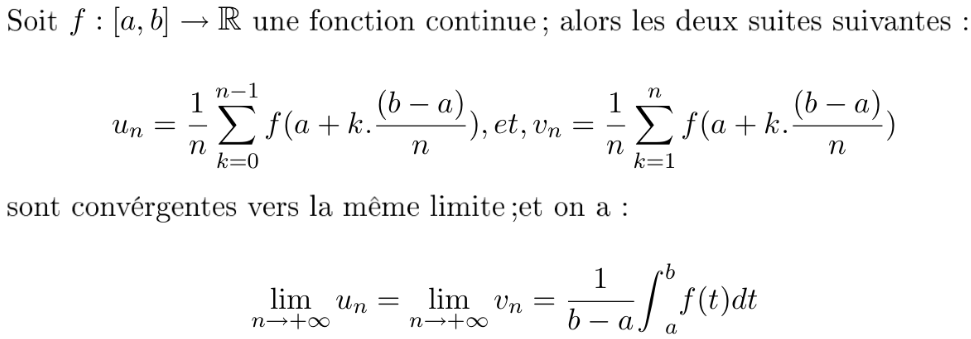
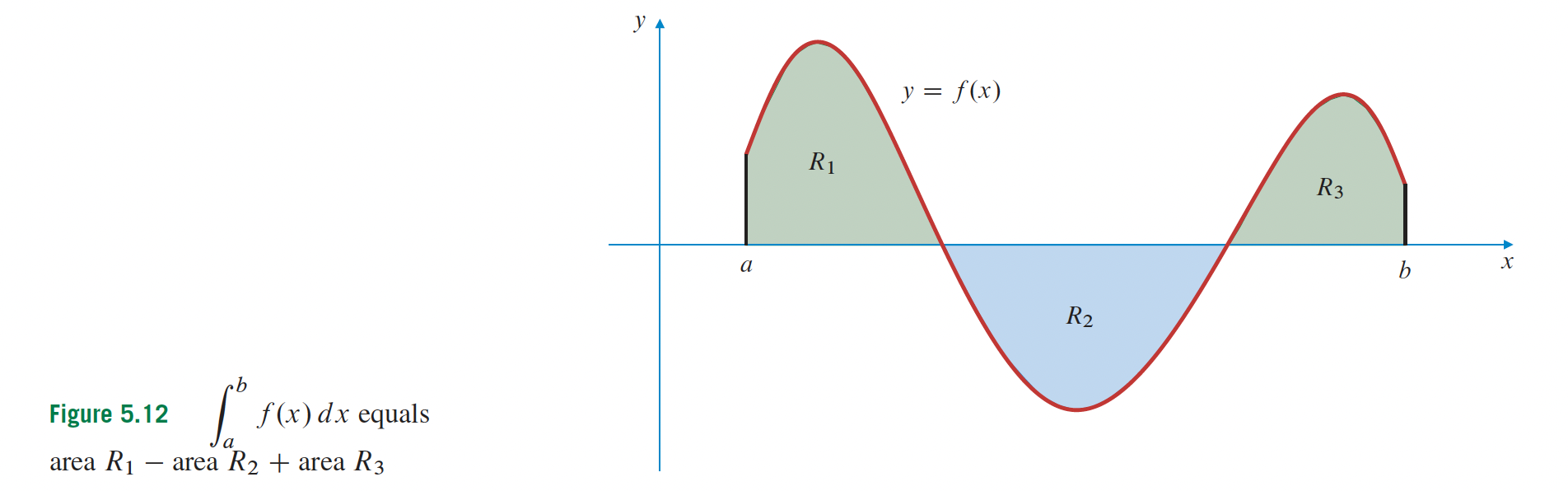
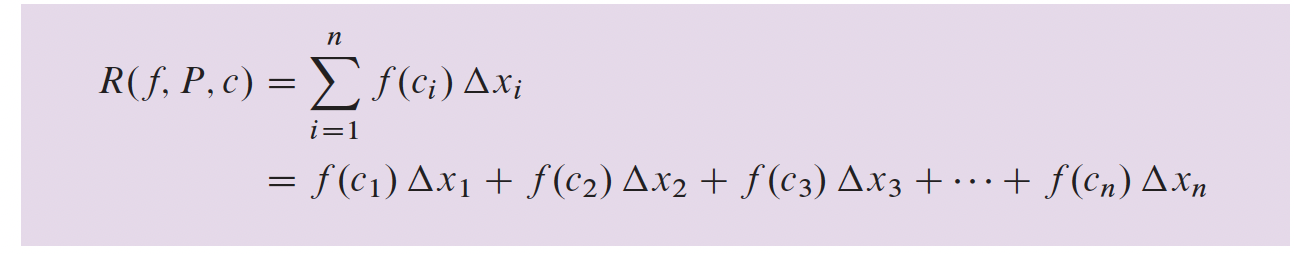
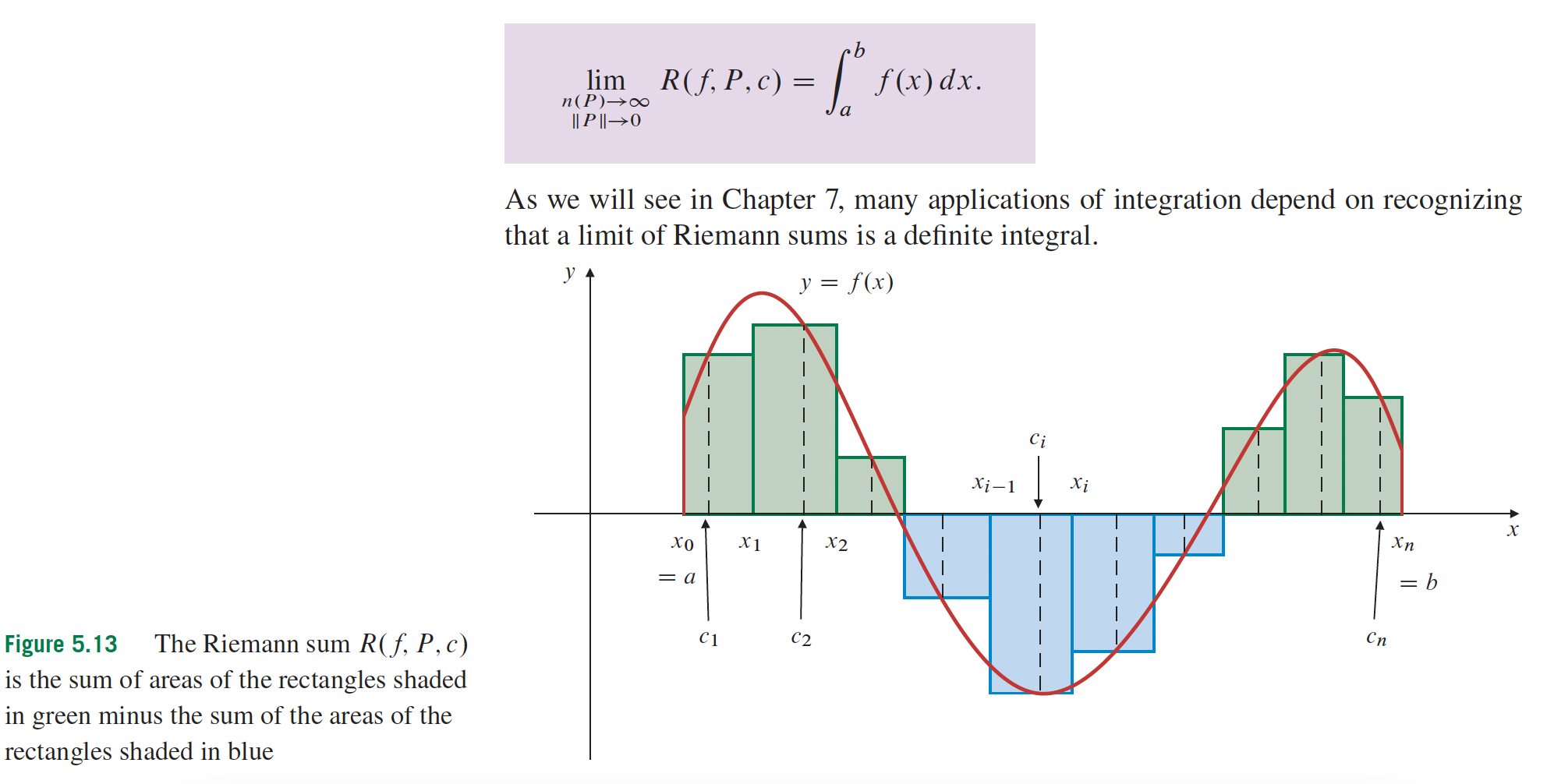
p. 309